TopOpt — Topology Optimization in Python¶


- Free Software: MIT License
- Github Repository: https://github.com/zfergus/topopt
Warning
This library is in early stages of development and consequently the API may change to better improve usability.
Topology optimization is a form of structure optimization where the design variable is the topology of the structure. Topological changes are achieved by optimizing the material distribution within a given design space.
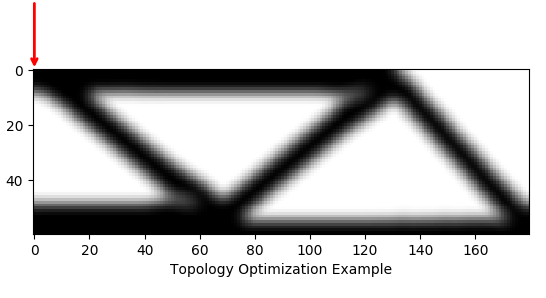
TopOpt is a python library for topology optimization. TopOpt contains common design problems (e.g. minimum compliance) solved using advanced methods (e.g. Method of Moving Asymptotes (MMA)). Using TopOpt we can optimize the classic Messerschmitt–Bölkow–Blohm (MBB) beam in a few lines of code:
import numpy
from topopt.boundary_conditions import MBBBeamBoundaryConditions
from topopt.problems import ComplianceProblem
from topopt.solvers import TopOptSolver
from topopt.filters import DensityBasedFilter
from topopt.guis import GUI
nelx, nely = 180, 60 # Number of elements in the x and y
volfrac = 0.4 # Volume fraction for constraints
penal = 3.0 # Penalty for SIMP
rmin = 5.4 # Filter radius
# Initial solution
x = volfrac * numpy.ones(nely * nelx, dtype=float)
# Boundary conditions defining the loads and fixed points
bc = MBBBeamBoundaryConditions(nelx, nely)
# Problem to optimize given objective and constraints
problem = ComplianceProblem(bc, penal)
gui = GUI(problem, "Topology Optimization Example")
topopt_filter = DensityBasedFilter(nelx, nely, rmin)
solver = TopOptSolver(problem, volfrac, topopt_filter, gui)
x_opt = solver.optimize(x)
input("Press enter...")
Output:
Development Status¶
TopOpt is in early stages of development and only features a limited set of finite element mesh options, optimization problems, and solvers. The following is a list of current and future features of TopOpt:
Meshes¶
- ✅ 2D regular grid
- ⬜ 2D general mesh
- ⬜ triangle mesh
- ⬜ quadrilateral mesh
- ⬜ 3D regular grid
- ⬜ 3D general mesh
- ⬜ tetrahedron mesh
- ⬜ hexahedron mesh
Problems¶
- ⬜ compliance
- ✅ linear elasticity
- ⬜ non-linear elasticity
- ⬜ stress
- ⬜ thermal conductivity
- ⬜ fluid flow
Solvers¶
- ⬜ optimality criterion
- ✅ method of moving asymptotes (MMA)
- ⬜ genetic algorithms